Primer modelo matemático de la transmisión de una enfermedad infecciosa.
“Simplemente deseo que,en un asunto que tanto afecta al bienestar de la humanidad,no se tome ninguna decisión sin todo el conocimientoque un pequeño análisis y cálculo pueden proporcionar”
D. Bernoulli (1760)
Tal día como hoy, en 1700, nació Daniel Bernoulli en Groninga (Países Bajos). En realidad su fecha de nacimiento fue el 29 de enero ya que en la zona protestante de Holanda el calendario juliano siguió aplicándose hasta el 30 de junio de ese año.
Perteneció al linaje matemático de los Bernoulli que formaron parte de la élite de los hombres de ciencia europeos en la segunda mitad del s. XVII y todo el s. XVIII, época de vertiginoso desarrollo económico, científico y tecnológico. Médico, matemático y físico, aunó el saber teórico y sus aplicaciones prácticas.
Por sus características personales y por la época en la que vivió, gran parte de los trabajos científicos de Daniel Bernoulli, como sus aportaciones a la dinámica de fluidos o al problema de la cuerda vibrante, son ejemplos paradigmáticos de modelización matemática; identificar un problema, descubrir su esencia matemática, encontrar la forma más simple de solucionarlo utilizando las herramientas proporcionadas por las matemáticas, e interpretar los resultados en el contexto del problema.
«Essai d’une nouvelle analyse de la mortalité causée par la petite vérole et des avantages de l’inoculation pour la prévenir»
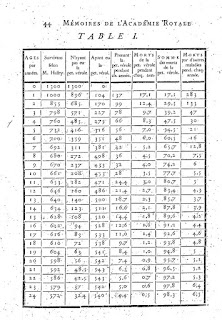
Entre sus numerosas e importantes aportaciones científicas elaboró el primer modelo matemático describiendo la transmisión de una enfermedad infecciosa, presentado en la Real Academia de Ciencias de París en 1760 y publicado en 1766.
Utilizando los datos de población recopilados en 1693 por Halley (conocido especialmente por el estudio del cometa que hoy lleva su nombre) y estimando los parámetros de incidencia y letalidad del modelo, aplicó el cálculo infinitesimal para cuantificar las muertes producidas por la viruela, en una época en la que era desconocida la causa de dicha enfermedad. Hoy hablaríamos de “minería de datos”.
Calculó el aumento de la esperanza de vida y de las cantidades de personas que alcanzarían ciertas edades en una población no afectada por la viruela y en una sistemáticamente variolizada, teniendo en cuenta los riesgos de la inoculación que se efectuaba en aquella época.
Usó sus resultados para argumentar las ventajas de la variolización con el objetivo de influir a favor de la vacunación contra la viruela de toda la población.
La viruela fue declarada como erradicada a nivel mundial por la OMS en 1980, gracias a las campañas de vacunación, la vigilancia y las medidas de prevención emprendidas para contener los focos epidémicos, así como la mejor información suministrada a las poblaciones afectadas. No puede afirmarse lo mismo de la oposición en los países occidentales desarrollados a la aplicación de vacunas, a pesar de los avances científicos y de la extensión de la educación a toda la población.
Desmos permite experimentar fácilmente con valores de tasas de infección y recuperación/mortalidad distintos a los estimados por Bernoulli.
No hay comentarios:
Publicar un comentario